B Tree
1. m-way search tree
Disk access is much slower than memory access. and disk is partitioned into blocks (pages) and the access time of a word is the same as that of the entire block containing the word.
so, binary trees are not quite appropriate for data stored on disks
we need to reduce the number of disk access → make each node of the tree wider
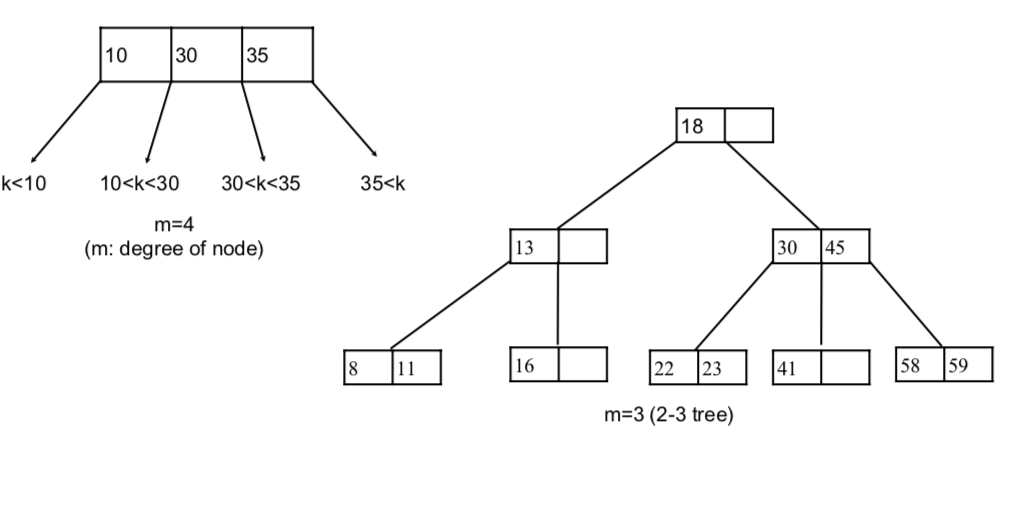
2. B-tree
: B-트리는 자료를 정렬된 상태로 보관하고, 삽입 및 삭제를 대수 시간에 할 수 있는 자료구조로, 데이터베이스와 파일 시스템에서 널리 사용된다.
1. definition
a B-tree of order m is an m-way search tree with the following properties
- the root is either a leaf or has at least 2 children
- all non-leaf nodes (except the root) have between ⎡m/2⎤ and m children
- all leaves are at the same level
for example,
- when m=2, full binary tree
- when m=3, all internal nodes of B-tree have a degree of either 2 or 3 (2-3tree)
- when m=4, all internal nodes of B-tree have a degree of 2, 3, or 4 (2-3-4 tree)
2. usage
- number of disk access is O(log_m N)
- each disk access requires O(log m) overhead to determine the direction to branch, but this is done in main memory without a hard disk access, thus negligible.
- m can be determined as large as possible, but it must still be small enough so that an internal node can fit into one disk block.
- m is typically between 32 and 256.
- often one or two levels of internal nodes reside in main memory.
Ref